CAN, atomic broadcast and Buridan's Ass

Atomic broadcast is a really, really useful thing when building a highly robust distributed real-time control system. The basic idea is that when a message is broadcast, either everyone in the system gets the message or no-one gets it¹. It’s a fundamental building block of fault tolerant systems, and also it really simplifies application design: if an application gets a notification that the message has been sent then it knows that all receivers got the message and will act on the same data. This is particularly useful if multiple nodes are acting on a mechanically linked system and need to act together, for example, controlling individual electric motors in each wheel of a vehicle.

There have been lots of projects over the years for building atomic broadcast on top of existing communications technologies. One of the earliest was the SIFT project (PDF). SIFT stands for Software Implemented Fault Tolerance and the project was concerned with using software to turn conventional computing hardware into robust hardware for aircraft control systems. Leslie Lamport worked on the SIFT project on the problem of distirbuted consensus and later published the now-famous Byzantine Generals Problem (which today is famous in the Bitcoin world, where the problem is solved with a blockchain). But arguably Leslie Lamport’s most important piece of work is the formulation of Buridan’s Principle (PDF). The principle is named after Buridan’s Ass, the donkey that starves to death because it is equidistant between two piles of hay and cannot decide which one to eat. The principle is simply stated:

A discrete decision based upon an input having a continuous range of values cannot be made within a bounded length of time.

While it might appear to be just a theoretical problem, it turns up all over the place. In digital circuit design where a flip-flop must latch an asynchronous input it is known as metastability (this is a common bear trap for beginners in chip design). It doesn’t mean that a discrete decision can’t be made, just that it’s not possible to bound the length of time to make the decision.

This puts limits on the properties of an atomic broadcast (which is, effectively, a distributed consensus problem): it is possible to ensure that every node sees the same data in a message, but it’s not possible to do it so that every node sees it at the same time.

Let’s look at this with a more concrete example: how to use a software layer on top of Ethernet to provide atomic broadcast. Ethernet doesn’t do much to help here. All Ethernet does is include a CRC check to see if a frame has been corrupted. Receivers simply throw the frame away if it’s bad and let software worry about it. So the software to implement atomic broadcast on Ethernet does something like this:

1. The sender transmits an Ethernet frame. It is broadcast on the bus, possibly going to a switch that forwards a copy to other bus segments (depending on the topology of the network)
2. When a receiver gets an Ethernet frame it always then sends an ACK frame back to the sender
3. The sender collates all the ACK frames until one has been seen from each receiver, then notifies the application that the message has been sent
4. If not all the ACKs have been received by some timeout then the sender goes back to step (1) and re-sends the Ethernet frame

The video below gives an example of one round of the above algorithm:

The difficult part of this algorithm is setting the timeout: it needs to be longer than the longest Ethernet frame latency from the sender to any receiver, and then from the receiver back to the sender. If the timeout is set too short then it will trigger as a false positive, and this could lead to a cascade of messages and acknowledgements (that would be bad, not least because it would be an intermittent fault and maybe only show up after deployment).

This isn’t straightforward to do in Ethernet because it was never designed for real-time systems - it was conceived as a general computer networking protocol, and doesn’t have deterministic arbitration (although there are various approaches used to patch over this problem, such as running a time-triggered protocol over the top of Ethernet).

The algorithm has a loop in it, which illustrates how Buridan’s Principle holds: the algorithm is unbounded. The best we can do is pick a probability that is acceptable then determine the number of loops based on that probability. The designer can then go on to assume worst-case latencies of Ethernet frames based on this loop bound (in essence this is also how the metastability problem in chip design is addressed).

There is another fundamental property of atomic broadcast that the algorithm illustrates: every receiver gets the same message, but some receivers may get it more than once. This has to be resolved, usually with a sequence number in the message so that receivers discard duplicates.

It’s fairly easy to see that Ethernet has poor real-time performance for atomic broadcast: each round of the algorithm can take many milliseconds. And we may find that the probability of losing a frame isn’t just down to the chance of noise causing a CRC error but also the highly unpredictable chance of a switch discarding a frame due to a buffer overrun.

Ethernet really is not great for distributed real-time systems, where message latencies are the most important thing. For sure, Ethernet has a lot of bandwidth but the frame latencies are high. Compare this to CAN, where the bandwidth is much lower (at least an order of magnitude lower) but the latencies for urgent frames are much shorter. To use an analogy that Andy Tanenbaum would surely approve of, Ethernet has the bandwidth and latency of a station wagon full of tapes, whereas CAN has the bandwidth and latency of an SMS message (it should be clear which is preferable to use to tell someone your house is on fire..)

So let’s see how atomic broadcast works on CAN. Well, it’s easy: the CAN protocol has atomic broadcast built in. All CAN frames are sent atomically: when the CAN controller at a sending node marks the frame as ‘sent’ then it has arrived OK at every other node on the bus. Isn’t that cool? In short, CAN doesn’t lose frames: they are always delivered.

Let’s have a quick look at how CAN does this. An example CAN frame is shown below:

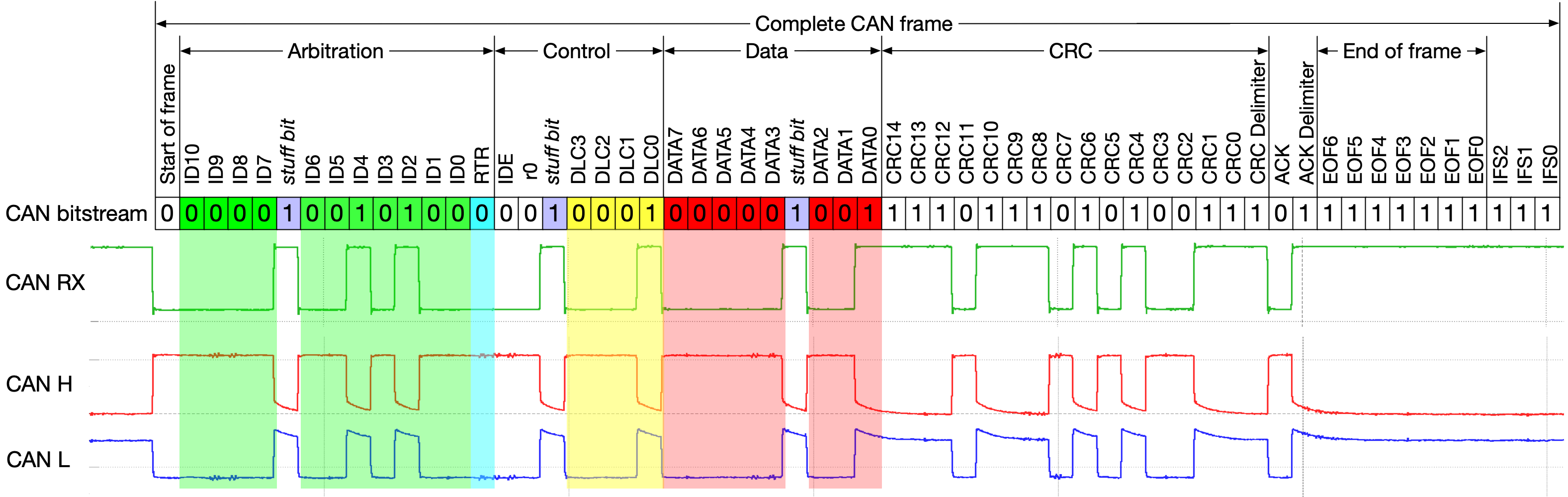
(Note that this is a re-rendering of the example CAN frame on Wikipedia - that frame is actually broken and lists the wrong CRC)

CAN has an ACK field, a single bit that the transmitter sends as a 1 but expects receivers to overwrite with a 0. If there are no receivers on the bus then the sending CAN controller triggers a CAN error and the frame is re-sent. This will go on forever until the frame is acknowledged. So the sending application won’t get a ‘sent’ indicator if it is on a bus by itself.

The ACK field is only one bit, so there’s no way to tell from that if all the receivers got the frame. This is solved by the error handling part of the CAN protocol: if a receiving CAN controller sees a corrupted frame (e.g. the computed CRC fails to match the received CRC) then not only does it not write a 0 bit into the ACK field, it also triggers an error frame that destroys the ongoing transmission of the CAN frame. This causes all controllers on the bus to resync, and for the sender to re-send the frame (technically, the sending CAN controller keeps the frame pending so that it will be re-entered into arbitration and, in due course, transmitted again).

So CAN automatically provides atomic broadcast for every frame. Probably there are a whole bunch of applications using CAN that actually rely on this property but don’t know they do - it all just works.

Even though CAN has atomic broadcast built in to the CAN hardware, there’s no escaping Buridan’s Principle. The CAN protocol defines a frame as ‘received OK’ when the second-to-last bit of EOF (EOF1) is received OK (i.e. received as a 1). But it defines ‘transmitted OK’ when the last bit of EOF (EOF0) is transmitted OK (i.e. received on loopback as a 1). A receiver that sees a local error in EOF1 (i.e. it sees a 0 bit, and all the others see a 1) will signal an error by sending six 0 bits in a row. This forces EOF0 to be 0, which causes the transmitter to see an error. That will result in the frame being re-sent. But all the other receivers already received the frame OK (because they read EOF1 as 1). So they will see the same frame again. This is the same problem we saw with the atomic broadcast algorithm for Ethernet: some receivers will see the frame more than once. In CAN this is called the CAN double receive problem, and the CAN specification actually explicitly points this out:

The trace below shows this happening for real on our benchtop testbed:

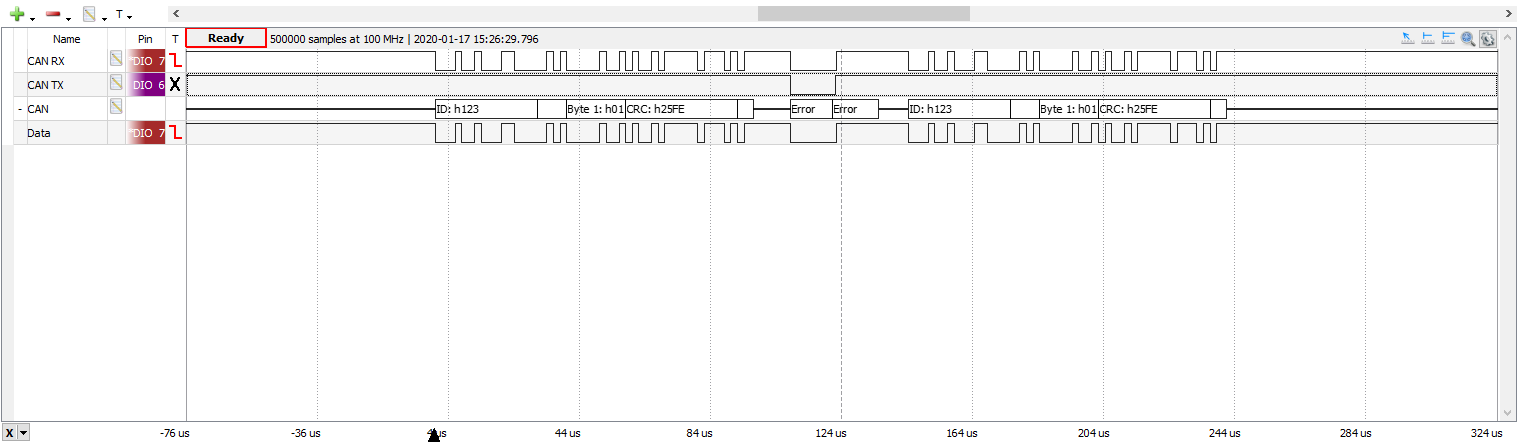
An error occurs in EOF0 and the frame is retransmitted. But this is what happens at a receiver:

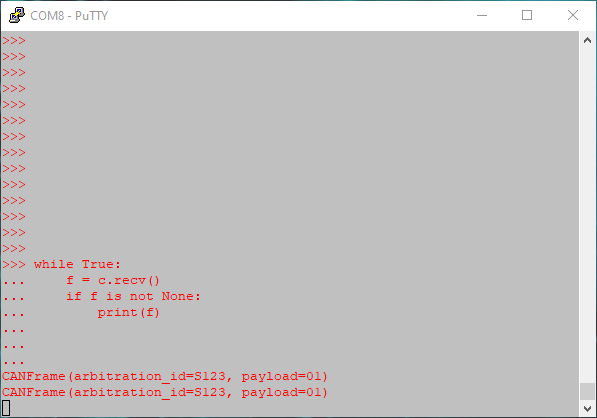
The receiver in the above example is a microcontroller running MicroPython, with a REPL command line and showing a Python API to CAN drivers. The while loop acts as a simple bus analyzer, and it shows that the frame was received twice, even though it was only sent once.

The resolution of this is the same as our Ethernet example earlier: to include a sequence number in the CAN frame payload and for the receiver software to discard duplicates. You might be wondering why the CAN protocol doesn’t specify the CAN hardware handle this automatically, but it turns out to be quite tricky to resolve in hardware due to the way CAN buffering of frames works (the sequence number is per frame and the hardware would have to interact with the frame buffers in a way it doesn’t today).

The window in which a bit error has to occur to trigger the double receive problem is actually quite small: just one bit. If bit errors have uniform probability then the double receive problem will occur at a rate about two orders of magnitude less frequent, so it’s possible that this issue is too rare for anyone to spot or care about, and few higher level protocols for CAN include a sequence number.

From a security perspective we can’t accept the above probability calculation: a hacker’s job is to drive the probability of an event to 1, and we used the CANHack toolkit to produce the trace above by injecting a 0 in EOF0 to force the double receive to happen. So if there is a risk of a malefactor gaining access to the CAN bus then for security reasons it’s best to actually care about this.

CAN’s atomic broadcast is really useful: it means that CAN never drops a frame, it always gets through to every controller on the bus. There is no need for anyone acknowledgement frames because once the sender gets ‘TX OK’ then the frame had to be received at all the CAN controllers on the bus.

But there are a couple of caveats. Firstly, if a node has fallen off the bus (e.g. the wire to it got cut) then the atomicity is lost. This situation has to be handled by some other means (normally this is called group membership and it can be done in software by sending a regular heartbeat message). Secondly, being received by the CAN state machine isn’t the same as being received by the application software. It’s possible to screw up the buffering so that there’s no place to put an incoming CAN frame and it has to be discarded (or overwrite an earlier frame). This may or may not be a problem, depending on the application, but if it is then the buffering needs to be designed properly (how that’s done is another story, a tale of timing analysis for CAN and understanding the worst-case frame arrival patterns).

To summarize:

• Atomic broadcast is a really, really useful thing for building robust distributed real-time control systems
• CAN provides atomic broadcast for all frames, which is really great
• There’s wrinkle in CAN’s atomic broadcast due to the double receive problem, thanks to Buridan’s Ass and the way the Universe works
• Ethernet sucks for robust distributed real-time control systems with tight latency requirements